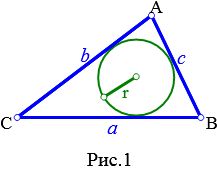
Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).
 |
Можно дать и другое определение окружности, вписанной в треугольник.
Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.
При этом треугольник называется треугольником описанным около окружности. Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.
Теорема 1. В любой треугольник можно вписать окружность.
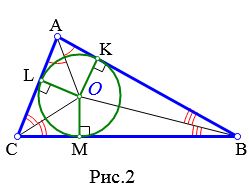 |
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.
Замечание 1. В любой треугольник можно вписать только одну окружность.
Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.
Смотрите также: