Теорема 1. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
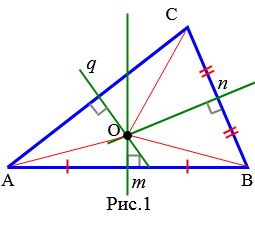 |
Доказательство. Пусть \( \small m \) и \( \small n \) серединные перпендикуляры сторон \( \small AB \) и \( \small BC \) треугольника \( \small ABC, \) соответственно (Рис.1). Покажем, сначала, что они пересекаются. Предположим, что \( \small m \) и \( \small n \) параллельны. Тогда прямая \( \small AB, \) которая перпендикулярна к прямой \( \small m, \) перпендикулярна и к прямой \( \small n.\) Получается, что через точку \( \small B \) проходят две прямые \( \small AB \) и \( \small BC, \) которые перпендикулярны к прямой \( \small n. \) Но это невозможно. Следовательно прямые \( \small m \) и \( \small n \) пересекаются в некоторой точке \( \small O. \)
Поскольку точка \( \small O \) находится на серединном перпендикуляре к отрезку \( \small AB ,\) то равноудалена от точек \( \small A \) и \( \small B. \) Тогда \( \small AO=BO. \) Аналогично \( \small BO=CO. \) Следовательно \( \small AO=CO, \) то есть точка \( \small O \) находится на серединном перпендикуляре отрезка \( \small AC. \) Получили, что все три серединных перпендикуляра \( \small m, \ n, \ p \) пересекаются в точке \( \small O. \)