С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть смотрите ниже.
Пусть известны площадь и высота ромба (Рис.1).
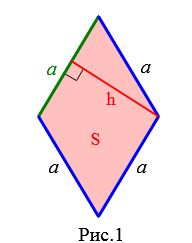 |
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| \(\small a=\frac{\large S}{\large h}.\) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
| \(\small S=a \cdot h.\) |
Откуда легко вывести формулу (1).
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
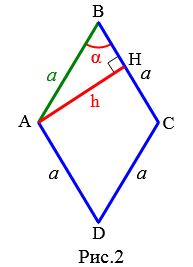 |
Для прямоугольного треугольника AHB применим теорему синусов:
| \(\small \frac{\large a}{\large \sin 90°}=\frac{\large h}{\large \sin \alpha}.\) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| \(\small a=\frac{\large h}{\large \sin \alpha}.\) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: \(\small \angle C=180°-\alpha.\) Следовательно \(\small \sin \angle C=\sin(180°-\alpha)=\sin \alpha.\) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
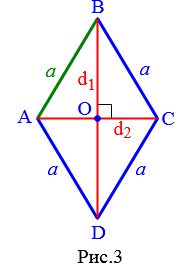 |
Применим к прямоугольному треугольнику AOB теорему Пифагора:
| \(\small a^2= \left( \frac{\large d_1}{\large 2} \right)^2+\left( \frac{\large d_2}{\large 2} \right)^2.\) |
Откуда:
| \(\small a= \frac{\sqrt{\large d_1^2+d_2^2}}{\large 2} \) | (3) |
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
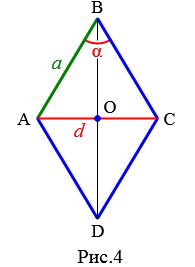 |
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
| \(\small \frac{\large a}{\large \sin 90°}=\frac{\large \frac{d}{2}}{\large \sin \frac{\alpha}{2}}.\) |
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| \(\small a=\frac{\large d}{\large 2 \ \cdot \ \sin \frac{ \alpha}{ 2}}.\) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| \(\small \sin \frac{ \alpha}{ 2}=\sqrt{\frac{\large 1-\cos \alpha}{\large 2 }}.\) | (5) |
Подставляя (5) в (4), получим:
| \(\small a=\frac{\large d}{\large 2 \ \cdot \ \sqrt{\frac{\large 1-\cos \alpha}{\large 2 }}}.\) |
или
| \(\small a=\large \frac{ d}{ \sqrt{ 2-2 \ \cdot \ \cos \alpha}}.\) | (6) |
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
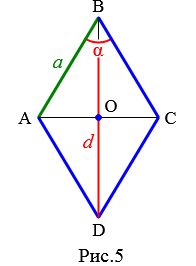 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| \(\small \frac{\large OB }{\large a} =\cos \angle ABO.\) | (7) |
Учитывая, что \( \small BO=\frac{\large d}{\large 2}\) и \( \small \angle ABO=\frac{\large \alpha}{\large 2}\), формулу (13) можно записать так:
| \(\small \frac{ \large \frac{\large d }{\large 2} }{\large a}= \cos \frac{\large \alpha}{\large 2} .\) |
или
| \(\small a=\frac{\large d}{\large 2 \ \cdot \ \cos \large \frac{ \alpha}{ 2}}.\) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| \(\small \cos \frac{ \alpha}{ 2}=\sqrt{\frac{\large 1+\cos \alpha}{\large 2 }}.\) | (9) |
Подставляя (9) в (8), получим:
| \(\small a=\frac{\large d}{\large 2 \ \cdot \ \sqrt{\frac{\large 1+\cos \alpha}{\large 2 }}}.\) |
или
| \(\small a=\large \frac{ d}{ \sqrt{ 2+2 \ \cdot \ \cos \alpha}}.\) | (10) |
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| \(\small S= 2 \cdot a \cdot r.\) | (11) |
Из формулы (11) получим:
| \( \small a=\frac{\large S}{\large 2 \ \cdot \ r} \) | (12) |
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| \(\small S= a^2 \cdot \sin \alpha.\) | (13) |
Из формулы (13) найдем a:
| \( \small a=\frac{\large S}{\large \sin \alpha} \) | (14) |
Получили формулу сторон ромба через площадь и угол.