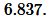С помощю этого онлайн калькулятора можно найти неизвестную сторону прямоугольного треугольника используя теорему Пифагора. Теоретическую часть и численные примеры смотрите ниже.
Теорема 1 (Теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
  |
Доказательство (метод площадей). Пусть задан прямоугольный треугольник с катетами a и b и гипотенузой c (Рис.1). Докажем, что \( \small c^2=a^2+b^2. \)
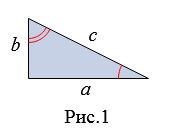
Построим квадрат со стороной a+b из четырех таких прямоугольных треугольников (Рис.2). Тогда внутренний белый четырехугольник будет квадратом со стороной c.
Действительно. В прямоугольных треугольниках (Рис.2) \( \small \angle 1 +\angle 2=90° \) Следовательно, каждый угол квадрата со стороной c равен \( \small \angle 3=180°-(\angle 1 +\angle 2)=180°-90°=90°.\)
Далее, площадь квадрата со стороной a+b равна:
| \( \small S_{a+b}=(a+b)^2. \) | (1) |
Площадь квадрата со стороной c равна:
| \( \small S_с=с^2. \) | (2) |
Площадь каждого прямоугольного треугольника на рисунке 2 равна:
| \( \small S=\frac12ab. \) | (3) |
Площадь квадрата со стороной a+b равна сумме площади квадрата со стороной c и четырех площадей прямоугольных треугольников c катетами a и b:
| \( \small S_{a+b}=S_c+4 \cdot S \) | (4) |
Подставляя (1)-(3) в (4), получим:
| \( \small (a+b)^2=с^2+4 \cdot \frac12ab, \) |
| \( \small a^2+2ab+b^2=с^2+2ab, \) |
\( \small a^2+b^2=с^2. \) |
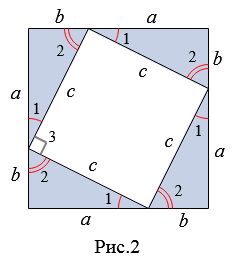
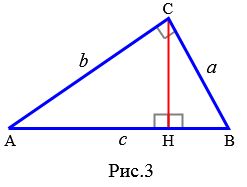
Доказательство (через подобные треугольники). Пусть задан прямоугольный треугольник ABC с катетами a и b и гипотенузой c (Рис.3). Докажем, что \( \small c^2=a^2+b^2. \) Проведем высоту CH. Прямоугольные треугольники ACB и CHB подобны по двум углам: \( \small \angle ACB= \angle CHB=90°, \ \angle B -\)общий (см. стратью на странице Подобные треугольники. Признаки подобия треугольников).
 |
Тогда
| \( \small \frac{\large a}{\large c}=\frac{\large HB}{\large a} \) |
или
| \( \small a^2=c \cdot |HB| \) | (5) |
Прямоугольные треугольники ACB и AHC подобны по двум углам: \( \small \angle ACB= \angle AHC=90°, \ \angle A -\)общий.
| \( \small \frac{\large b}{\large c}=\frac{\large AH}{\large b} \) |
или
| \( \small b^2=c \cdot |AH| \) | (6) |
Сложив уравнения (5) и (6), получим
\( \small a^2+b^2=c \cdot |AH| +c \cdot |HB|=c( |AH|+|HB|)=c^2. \) |
Доказательство (Евклид). Пусть задан прямоугольный треугольник ABC с катетами a, b и гипотенузой c (Рис.4). Докажем, что \( \small c^2=a^2+b^2. \)
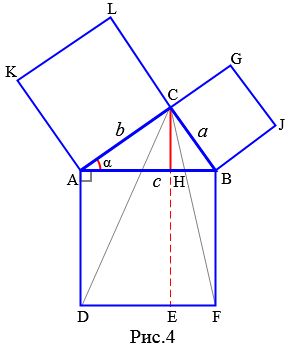 |
Достаточно доказать, что площадь квадрата ABFD равна сумме площадей ACLK и BCGJ:
| \( \small S_{ABFD}=S_{ACLK}+S_{BCGJ} . \) |
Площадь треугольника ACD по двум сторонам и углу между ними равен:
| \( \small S_{ACD}=\frac 12 \cdot AC \cdot AD \cdot sin(90°+\alpha) \) \( \small =\frac 12 \cdot AC \cdot AD \cdot sin \ \alpha . \) | (7) |
Учитывая, что \( \small \sin \angle ACH=\sin (90°-\alpha)=\sin \alpha, \) применим теорему синусов для прямоугольного треугольника ACH:
| \( \small \frac {\large AH}{\large \sin \angle ACH}=\frac {\large AH}{\large \sin \alpha} =\frac {\large AC}{\large \sin 90°} \) |
или
| \( \small \sin \alpha =\frac {\large AH}{\large AC}. \) | (8) |
Подставляя (8) в (7), получим:
| \( \small S_{ACD}=\frac 12 \cdot AH \cdot AD. \) | (9) |
Применим теорему синусов для прямоугольного треугольника ABC:
| \( \small \frac {\large AB}{\large \sin \angle C}=\frac {\large AB}{\large \sin 90°}=AB=\frac {\large AC}{\large \sin (90°-\alpha)}=\frac {\large AC}{\large \sin \alpha} \) |
или
| \( \small \sin \alpha =\frac {\large AC}{\large AB} \) | (10) |
Подставляя (10) в (7), получим:
| \( \small S_{ACD}=\frac 12 \cdot AC^2 \cdot \frac{\large AD}{\large AB} \) | (11) |
Учитывая, что \( \small AD=AB, \) получим:
| \( \small S_{ACD}=\frac 12 \cdot AC^2 . \) | (12) |
Из (9) и (12), имеем:
| \( \small AH \cdot AD=AC^2. \) | (13) |
Аналогично можно показать, что
| \( \small HB \cdot BF=BC^2. \) | (14) |
Сложив (13) и (14), получим:
| \( \small AH \cdot AD+HB \cdot BF=S_{ABFD}=AC^2+BC^2. \) |
или
\( \small c^2=b^2+a^2. \) |
Пример 1. Известны катеты прямоугольного треугольника \( \small a=\frac{5}{2}, \) \( \small b=\frac{3}{4}. \) Найти гипотенузу.
Решение: Для нахождения гипотенузы воспользуемся формулой Пифагора:
| \( \small c^2=a^2+b^2. \) |
Откуда:
| \( \small c=\sqrt{a^2+b^2}. \) | (15) |
Подставляя значения \( \small a \) и \( \small b \) в (15), получим:
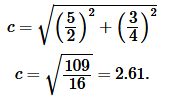 |
Ответ: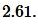
Пример 2. Известны катет \( \small a=\frac{3}{2} \) и гипотенуза \( \small c=7 \) прямоугольного треугольника. Найти неизвестный катет.
Решение: Для нахождения неизвестного катета воспользуемся теоремой Пифагора:
| \( \small c^2=a^2+b^2. \) |
Откуда:
| \( \small b=\sqrt{c^2-a^2}. \) | (16) |
Подставляя значения \( \small a \) и \( \small b \) в (16), получим:
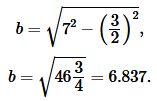 |
Ответ: