Теорема 1. Если квадрат одной стороны треугольника равен сумме квадратов других сторон, то треугольник прямоугольный.
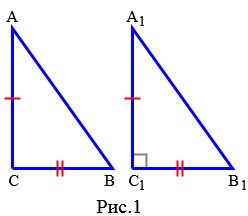 |
Доказательство. Пусть в треугольнике ABC выполнено условие \( \small AB^2=AC^2+BC^2 \)(Рис.1). Докажем, что угол \( \small C \) прямой. Рассмотрим прямоугольник \( \small A_1B_1C_1, \) у которого угол \( \small C_1 \) прямой и \( \small A_1C_1=AC, \) \( \small B_1C_1=BC \) (Рис.1). По теореме Пифагора для треугольника \( \small A_1B_1C_1, \) имеем \( \small A_1B_1^2=A_1C_1^2+B_1C_1^2=AC^2+BC^2. \) Но по условию теоремы \( \small AC^2+BC^2=AB^2. \) То есть \( \small A_1B_1^2=AB^2, \) или \( \small A_1B_1=AB. \) Тогда треугольники \( \small A_1B_1C_1 \) и \( \small ABC \) равны по трем сторонам, т.е. по третьему признаку равенства треугольников (см. статью Треугольники. Признаки равенства треугольников). Отсюда следует равность углов \( \small C \) и \( \small C_1. \)