

В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.
Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком "+", если эта точка и начало координат лежат по разные стороны прямой, и со знаком "−", если точка и начало координат лежат по одну сторону от прямой.
Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком "+", если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком "−", в противном случае.
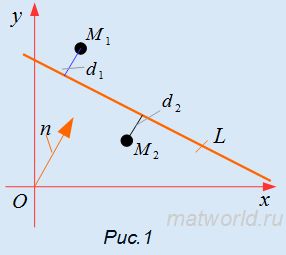
Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 и начало координат O лежат по разные стороны прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 и начало координат O лежат по одну сторону от прямой L.
 |
На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L
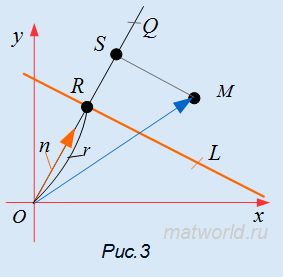
Рассмотрим нормальное уравнение прямой L (Рис.3):
| xcosφ+ysinφ−r=0. | (1) |
где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.
Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:
Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.
Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.
 |
Тогда
| δ=SR=OS−OR=OS−r. | (2) |
Но
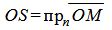 , , | (3) |
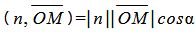 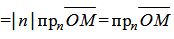 , , | (4) |
где n− единичный нормальный вектор прямой L, α−угол между векторами n и .
Из (3) и (4) следует:
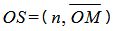 . . | (5) |
С другой стороны
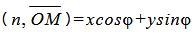 , , | (6) |
так как нормальный вектор прямой имеет координаты n={cosφ, sinφ}, а точка M − M(x, y).
Сопоставляя (2), (5) и (6), получим:
| δ=xcosφ+ysinφ−r. |
Теорема доказана.
Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M0(x0, y0) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M0:
| δ=x0 cosφ+y0 sinφ−r. |
Заметим, расстояние от точки M0 до прямой L будет равно модулю отклонения данной точки от прямой.
Пример 1. Задано нормальное уравнение прямой:
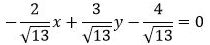 . . | (7) |
Найти отклонение точки M(5,-3) от прямой (7).
Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):
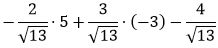 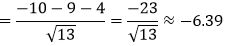 . . |
Ответ. Отклонение точки M(5,−3) от прямой (7) равно:
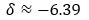 . . |
Пример 2. Задано общее уравнение прямой:
| 4x−3y+1=0. | (8) |
Найти отклонение точки M(1,1) от прямой (8).
Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье "нормальное уравнение прямой"). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:
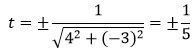 . . |
Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:
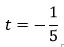 . . |
Умножив уравнение (8) на нормирующий множитель, получим:
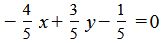 . . |
Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):
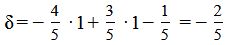 . . |
Ответ. Отклонение точки M(1,1) от прямой (8) равно:
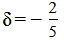 . . |