В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
| xcosφ+ysinφ−r=0, | (1) |
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором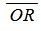 
. (Если точки O и R совпадают, то направление n можно взять произвольным).
 |
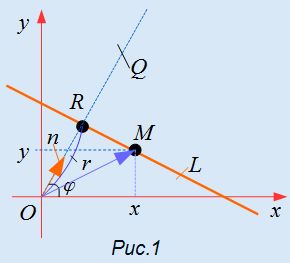Выразим уравнение прямой L через два параметра: длину отрезка 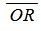и угол φ между вектором n и осью Ox.
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
| n={cosφ, sinφ}. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора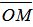 
на прямую R равна r, т.е.
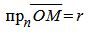 | (3) |
Скалярное произведение векторов n и 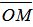имеет следующий вид:
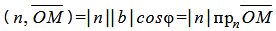 , | (4) |
где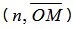 
− обозначен скалярное произведение векторов n и 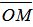, а | · |− норма (длина) вектора, α−угол между векторами n и .
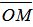Поскольку n единичный вектор, то (4) можно записать так:
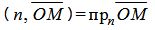 . | (5) |
Учитывая, что n={cosφ, sinφ},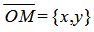 
, мы получим:
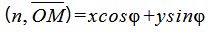 . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosφ+ysinφ=r |
или
| xcosφ+ysinφ−r=0. | (7) |
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой.
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
 ,  |
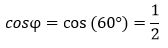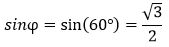Подставляя вычисленные значения в (7) получим:
 . |
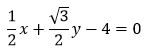Ответ:
| . |
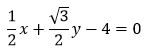Пусть на плоскости задано уравнение прямой в общем виде:
| Ax+By+C=0. | (8) |
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи "Общее уравнение прямой на плоскости"), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA)2+(tB)2=cos2φ+sin2φ=1. | (10) |
Упростим выражение и найдем t:
| t2A2+t2B2=t2(A2+B2)=1, |
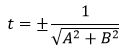 . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем.
Пример 2. Задано общее уравнение прямой
| 2x−3y+4=0. | (12) |
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
 |
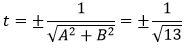Так как C>0, то знак t отрицательный:
 |
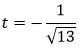Умножим уравнение (12) на t:
 |
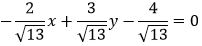Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
|
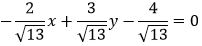Отметим, что число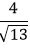 
является расстоянием от начала координат до прямой (12).