Суммой двух матриц A и B одних и тех же порядков m×n называется матрица C тех же порядков m×n, элементы cij которой равны
cij=aij+bij (i=1,2,...,m; j=1,2,...n).
Для обозначения суммы двух матриц используется запись:
C=A+B.
Из определения сложения матриц непосредственно следует, что эта операция обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойствами:
Здесь A, B, C произвольные m×n матрицы.
Рассмотрим пример сложения следующих двух матриц:
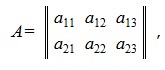
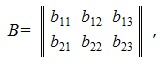
В результате сложения получим следующую матрицу:
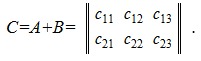
где c11=a11+b11, c12=a12+b12, c13=a13+b13, c21=a21+b21, c22=a22+b22, c23=a23+b23.
Рассмотрим следующий численный пример:
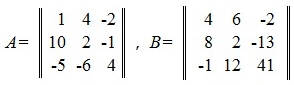
Сумма матриц A+B будет:
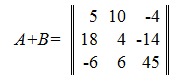
Для сложения матриц пользуйтесь матричным онлайн калькулятором.