Теорема 1. На сторонах AB и BC треугольника ABC отметим точки C1 и A1, соответственно, а на продолжении стороны AC − точку B1. Для того, чтобы точки A1, B1, C1 лежали на одной прямой, необходимо и достаточно, чтобы выполнялось равенство
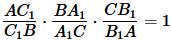 | (1) |
Доказательство. Необходимость. Докажем, что если точки A1, B1, C1 лежат на одной прямой, то выполняется равенство (1).
Из вершин треугольника ABC опустим перпендикуляры AM, BP, CQ на прямую B1C1 (Рис.1).
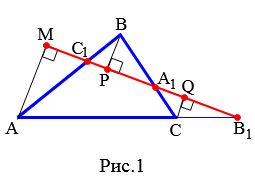 |
Тогда \( \small \angle AMC_1= \angle BPC_1=90°. \) Углы AC1M и BC1P вертикальные, поэтому \( \small \angle AC_1M= \angle BC_1P. \) Следовательно треугольники AMC1 и BPC1 подобны по первому признаку подобия треугольников. Отсюда имеем:
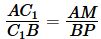 | (2) |
Аналогично, из подобия треугольников BPA1 и CQA1, получим
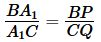 | (3) |
Из подобия треугольников B1QC и B1MA, получим
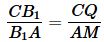 | (4) |
Перемножив левые и правые части равенств (2)−(4), получим:
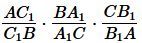 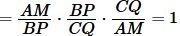 |
Достаточность. Докажем, что если выполняется условие (1), то точки A1, B1, C1 лежат на одной прямой.
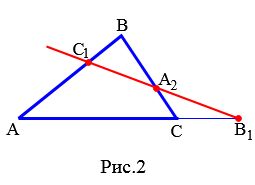 |
Пусть прямая C1B1 пересекает сторону BCтреугольника ABC в точке A2 (Рис.2). Так как точки C1, A2, B1 лежат на одной прямой, то выполнено следующее равенство (см. доказательство выше):
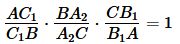 | (5) |
Сопоставляя (5) с (1), получим:
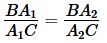 |
Как видно из последнего равенства, точки A1 и A2 делят отрезок C1B1 в одном и том же соотношении. А это значит, что эти точки совпадают. Следовательно точки A1, B1, C1 лежат на одной прямой.
Замечание 1. Теорема 1 справедлива и для случая, когда точки A1, B1, C1 лежат на продолжениях сторон треугольника ABC (Рис.3).
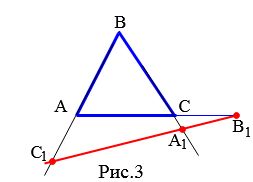 |