С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.
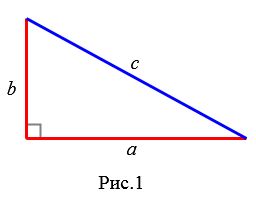 |
На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:
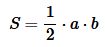 | (1) |
Пример 1. Известны катеты прямоугольного треугольника: 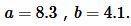 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения 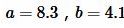 в (1), получим:
в (1), получим:
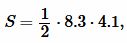 |
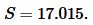 |
Ответ: 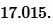
Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):
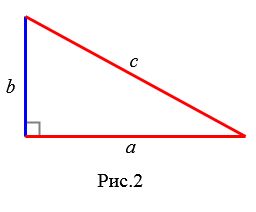 |
Найдем площадь треугольника. Из формулы Пифагора имеем:
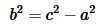 , , |
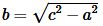 . . | (2) |
Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:
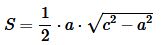 . . | (3) |
Пример 2. Известны катет и гипотенуза прямоугольного треугольника: 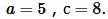 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значения 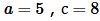 в (3), получим:
в (3), получим:
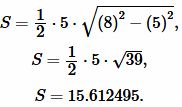 |
Ответ: 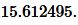
Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):
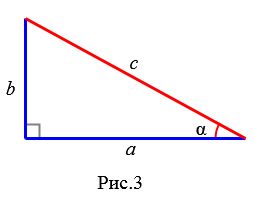 |
Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:
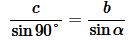 , , 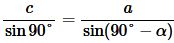 |
или
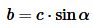 , , 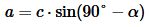 | (4) |
Подставим (4) в (1):
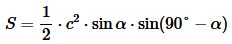 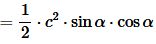 | (5) |
Из формулы произведения тригонометрических функций имеем:
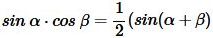 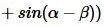 | (6) |
Подставим в (6) \( \small \beta=\alpha \):
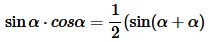 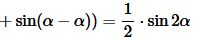 | (7) |
Применяя (7) относительно формулы (5), получим:
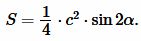 | (8) |
Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: 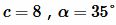 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения 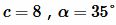 в (8), получим:
в (8), получим:
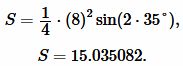 |
Ответ: 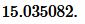
Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):
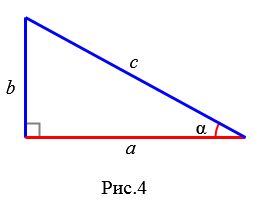 |
Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:
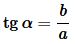 . . |
Откуда
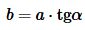 . . | (9) |
Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:
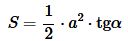 . . | (10) |
Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: 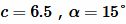 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения 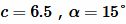 в (10), получим:
в (10), получим:
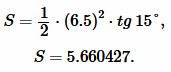 |
Ответ: 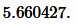
Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):
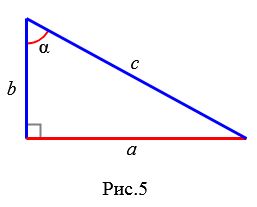 |
Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:
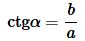 . . |
Откуда
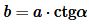 . . | (12) |
Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:
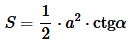 . . | (13) |
Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: 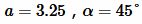 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 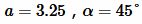 в (13), получим:
в (13), получим:
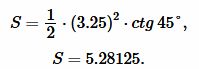 |
Ответ: 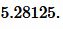
Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис.6):
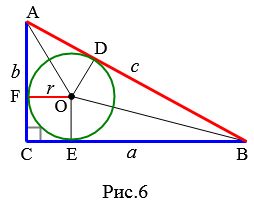 |
Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.
Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку 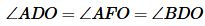
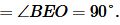 Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
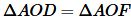 . . | (14) |
Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):
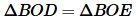 . . | (15) |
Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:
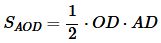 , , 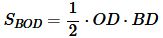 , , | (16) |
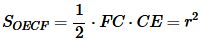 . . | (17) |
Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:
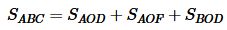 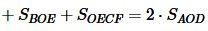 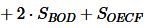 . . | (18) |
Подставляя (16), (17) в (18), получим:
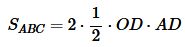 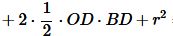 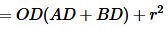 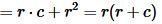 |
или
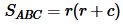 . . | (19) |
Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: 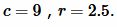 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения 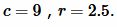 в (19), получим:
в (19), получим:
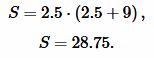 |
Ответ: 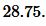
Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис.6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:
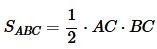 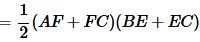 . . | (20) |
Учитывая, что 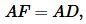
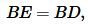
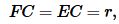
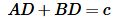 , (20) примет вид:
, (20) примет вид:
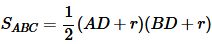 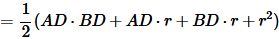 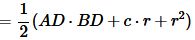 . . |
То есть
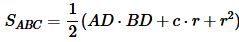 , , | (21) |
Сравнивая формулы (19) и (21) можем записать:
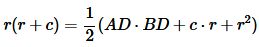 , , |
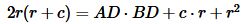 , , |
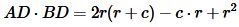 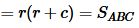 . . |
Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:
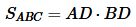 . . | (22) |
Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6) 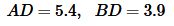 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения 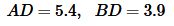 в (22), получим:
в (22), получим:
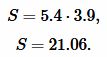 |
Ответ: 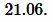
Смотрите также: