Пусть задана прямая a и точка A, не лежащая на этой прямой (Рис.1).
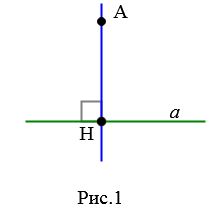 |
Отметим на прямой a точку H и соединяющие точки A и H. Отрезок AH называется перпендикуляром проведенным от точки A к прямой a, если прямые a и AH перпендикулярны. Точка H называется основанием перпендикуляра.
Теорема 1. Из точки, не лежащей на данной прямой можно провести перпендикуляр к этой прямой, и причем единственный.
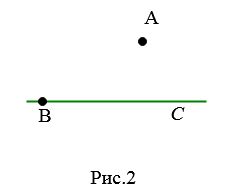
Доказательство. Пусть задана прямая BC и точка A, не лежащая на этой прямой (Рис.2).
 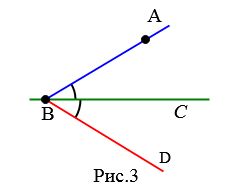 |
Докажем, сначала, что из точки A можно провести перпендикуляр к прямой BC. Проведем луч BA и отложим от луча BC угол DBC, равной углу ABC (Рис.3). Поскольку \( \small ∠ ABC=∠ DBC,\) то первый из них можно наложить на вторую. При этом точка A наложится на некоторую точку A1 луча BD (Рис.4).
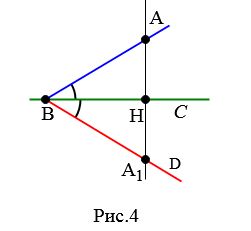 |
Обозначим через H точку пересечения прямых AA1 и BC. Таким образом при наложении угла ABC на угол DBC, точка A наложилась на точку A1. Тогда AH наложится на A1H, угол AHB наложится на угол A1HB. Следовательно \( \small ∠ AHB=∠ A_1HB.\) Но углы AHB и A1HB смежные, значит \( \small ∠ AHB+∠ A_1HB=180°.\) Таким образом \( \small ∠ AHB=∠ A_1HB=90°.\) Тогда AH пернпендикуляр к прямой BC от точки A, т.е. \( \small AH⊥ BC.\)
Докажем, далее, что из точки A можно провести только один перпендикуляр к прямой BC.
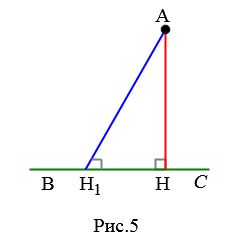 |
Предположим, что из точки A можно провести еще один перпендикуляр AH1 (Рис.5). Тогда получим, что две прямые AH и AH1 перпендикулярные к прямой BC пересекаются. Но это противоречит тому, что если две прямые перпендикулярны к третьей, то они не пересекаются (теорема 1 статьи Перпендикулярные прямые). Следовательно из точки A можно провести только один перпендикуляр к прямой BC.