Определение 1. Угол с вершиной в центре окружности, называется центральным углом окружности.
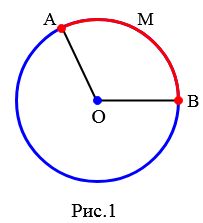
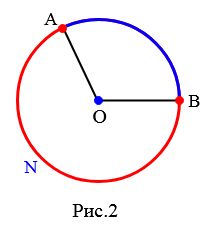
Пусть стороны центрального угла окружности, с центром в точке O пересекают окружность в точках A и B. Тогда центральному углу \( \small \angle AOB \) окружности соответствуют две дуги с концами A и B. Если угол AOB меньше 180°, то говорят, что дуга, расположенная внутри этого угла меньше полуокружности (дуга AMB Рис.1). Другая дуга, с концами A и B − больше полуокружности (дуга ANB Рис.2).
  |
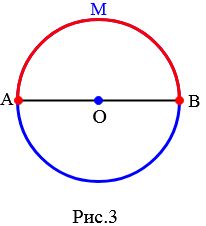
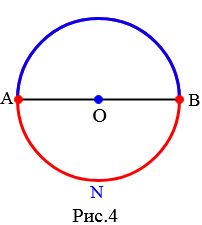
Если угол AOB развернутый, то ему соответствуют две полуокружности: полуокружность AMB Рис.3, и полуокружность ANB Рис.4
  |
Дугу окружности можно измерять в градусах.
Если дуга AB (AMB) окружности с центром O меньше полуокружности (Рис.1) или является полуокружностью (Рис.3 и Рис.4), то градусная мера дуги считается равной градусной мере центрального угла AOB.
Если дуга AB (ANB) больше полуокружности (Рис.2), то ее градусная мера считается равной \( \small \boldsymbol{ 360°-\angle AOB }.\)
Из вышеизложенного следует, что сумма градусных мер двух дуг окружности с общими концами равна 360°.
Градусная мера дуги AMB как и сама дуга, обозначается символом ◡AMB.
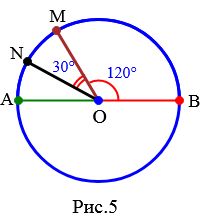 |
На рисунке 5 градусная мера дуги MB равна 120°. Кратко говорят: "дуга MB равна 120°" и пишут: ◡MB=120°. Дуга NMB равна 150°. На данном рисунке: \( \small ◡NAB=360°-\angle NOB \) \( \small =360°-(\angle NOM+\angle MOB) \) \( \small =360°-(30°+120°)=210° .\)