С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку "Перевести". Теоретическую часть и численные примеры смотрите ниже.
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·103+3·102+7·101+2·100.
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·103 +2·102 +8·101+7·100+9·10-1+2·10-2+3·10-3.
В общем случае формулу можно представить в следующем виде:
где Цn-целое число в позиции n, Д-k- дробное число в позиции (-k), s - система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления - из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления - из множества цифр {0,1}, в шестнадцатеричной системе счисления - из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1·26+0·25+1·24+1·23+1·22 +0·21+1·20+0·2-1+0·2-2+1·2-3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
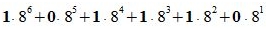 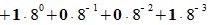 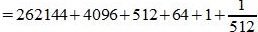 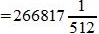 |
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
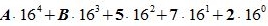 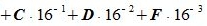 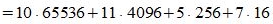 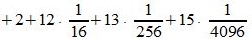 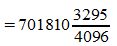 |
Здесь A -заменен на 10, B - на 11, C- на 12, F - на 15.
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления - последовательным делением целой части числа на основание системы счисления (для двоичной СС - на 2, для 8-ичной СС - на 8, для 16-ичной - на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
15910=100111112.
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
61510=11478.
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 - D. Следовательно наше шестнадцатеричное число - это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
0.21410=0.00110112.
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
0.12510=0.0012.
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0.21410=0.36C8B416.
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
0.51210=0.4061118.
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
159.12510=10011111.0012.
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
19673.21410=4CD9.36C8B416.