Скалярным произведением ненулевых векторов x и y называется произведение
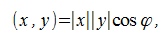 | (1) |
где |·|-модуль вектора, φ -угол между векторами.
Если x=0 или y=0, то скалярное произведение равно нулю.
Пусть в n-мерном пространстве задан ортонормированный базис
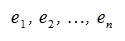
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть заданы векторы
  |
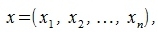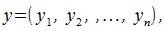тогда скалярное произведение (x,y) векторов x и y определяется соотношением:
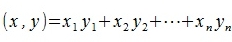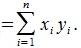  | (2) |
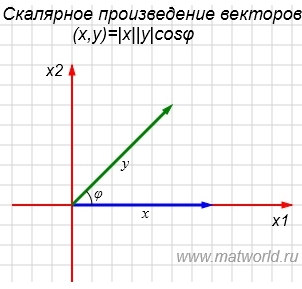
Рис. 1
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,0) и y=(5,5).
Для вычисления скалярного произведения методом (1), вычислим нормы векторов x и y:
  |
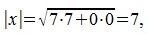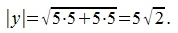Учитывая что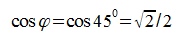 
, получим:
  |
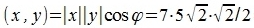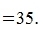Теперь вычислим скалярное произведение векторов x и y используя выражение (2):
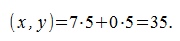
Получили одинаковые результаты, но посдедний вариант вычисления проще и не требует знания угла между векторами.
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x=AB и y=CD, где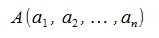 
,
,
,
.
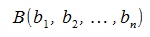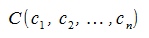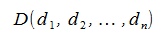Переместим векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x' и y' с координатами (т.е. с конечными точками):
  |
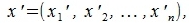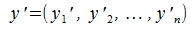где
  | |
  |
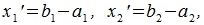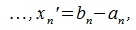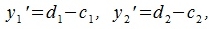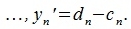Из выражения (1) видно, что скалярное произведение векторов x и y зависит только от нормы векторов и от угла между ними. Так как |x'|=|x| , |y'|=|y| и угол между векторами x' и y' равен углу между векторами x и y, следовательно
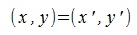
Учитывая (2) получаем:
  |
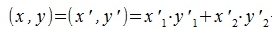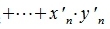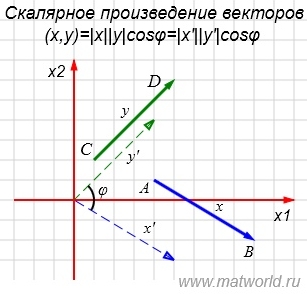
Рис. 2
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x=AB и y=CD, где A(4,1), B(9,-2), C(1,2), D(5,6).
Из выражения (1) видно, что скалярное произведение векторов x и y зависит только от нормы векторов и от угла между ними. Переместим параллельно векторы так, что их начальные точки совпали с началом координат. Тогда x'=(9-4, -2-1)=(5, -3), y'=(5-1, 6-2)=(4,4), |x'|=|x| , |y'|=|y| и угол между векторами x' и y' равен углу между векторами x и y. Следовательно
  |
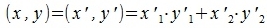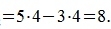