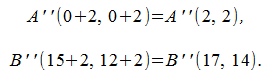Произведением вектора x на число β (x≠0, β≠0) называется вектор, модуль которого равен |x||β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β<0. Если x=0 и (или) β=0, то βx=0.
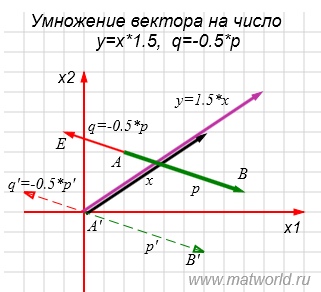
Рис. 1
На рисунке Рис. 1 вектор x умножен на число 1.5. Полученный вектор y' имеет то же направление, что и x т.к 1.5>0, и имеет длину 1.5 раз превысшающее длину x.
Вектор q имеет противополжное к p направление, т.к. вектор p умножено на отрицательное число -0.5, и имеет длину 2 раза меньше длины p.
Рассмотрим процесс умножения вектора на число.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть имеется вектор
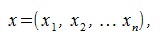
где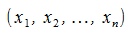 
координаты вектора x, и пусть β некоторое число. Тогда
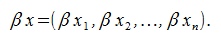
То есть для умножения вектора на число достаточно умножить каждый координат данного вектора на это число.
На рисунке Рис. 1 вектор x имеет координаты x=(6,4). Для умножения вектора x на число 1.5, умножим каждый координат вектора x на число 1.5:
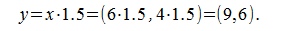
Вариант 2. Начальные точки векторов произвольные.
Пусть имеется вектор x, с начальной точкой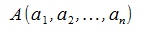 
и конечной точкой 
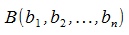. Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A.
Переместим вектор x на начало координат. Получим новый вектор x' с начальными и конечными точками:
  | |
 |
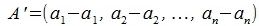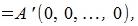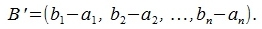Умножим x' на β:
  |
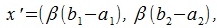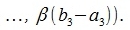Параллельно переместив начальную точку вектора x' на точку A, получим вектор x'' с начальными и конечными точками:
 | |
  |
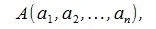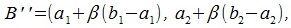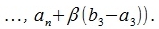На рисунке Рис. 1 вектор p=AB имеет координаты A(2,3) и B(8,1). Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p'=A'B' с координатами A'(0,0) и B'(8-2, 1-3)=B'(6,-2). Умножим вектор p' с числом -0.5:
  |
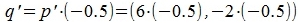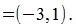Перемесив начальную точку вектора q' на точку A, получим вектор q=AE, где точка E имеет координаты:
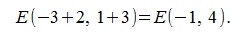
Операция умножения вектора на число обладает следующими свойствами:
1.β(x+y)=βx+βy (дистрибутивность относительно сложения векторов).
2. (α+β)a=αa+βa (дистрибутивность относительно сложения чисел).
3. α(βa)=(αβ)a (ассоциативность).
4. 1·a=a (умножение на единицу).
Пример 1. Умножить вектор y=(3,5,-6) на число 2.5.
Для умножения вектора y на число 2.5, просто умножаем каждый координат вектора y на данное число:  |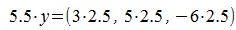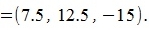
Пример 2. Умножить вектор x=AB на число 3, где A(2,2), B(7,6).
Переместим вектор AB на начало координат. Начальное и конечное точки перемещенного вектора будут:
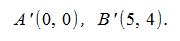
Умножив полученный вектор на число 3, изменяется расположение конечной точки B':
.
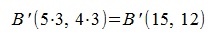Переместив вектор на точку A, получим вектор 3·x, со следующими начальной и конечной точками:
