Определитель матрицы

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

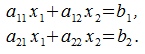(1)

Умножим обе части первого уравнения на a₂₂ а второе на -a₁₂ и сложим. Получим следующее уравнение

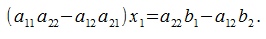
Далее, первое уравнение умножим на -a₂₁ а второе на a₁₁ и сложим:

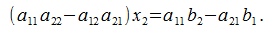
Пусть 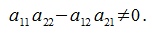Тогда решение системы (1) примет следующий вид:

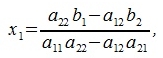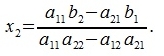Выражение 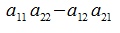называется определителем матрицы

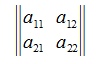
и обозначается:

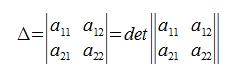
Нетрудно заметить, что

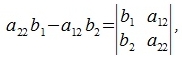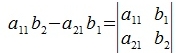Таким образом, решение системы линейных уравнений можно представить в виде:

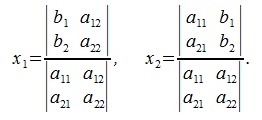
Рассмотрим случай из трех неизвестных и трех уравнений. Пусть дана система линейных уравнений

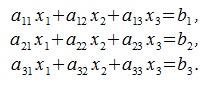(2)

Исключим неизвестные x₂ и x₃. Для этого умножим первое уравнение на a₂₂a₃₃-a₃₂a₂₃, второе на -(a₁₂a₃₃-a₁₃a₃₂), третье на a₁₂a₂₃-a₂₂a₁₃, и сложим:

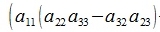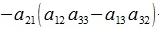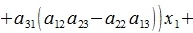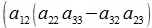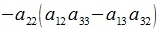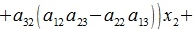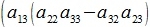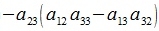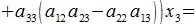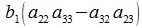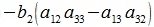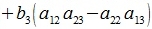Сделаем следующие обозначения:

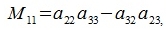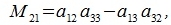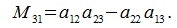Учитывая, что выражения перед элементами x₂ и x₃ равны нулю, имеем:

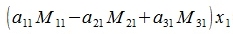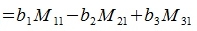Выражение 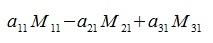называется определителем матрицы

(3)

и обозначается:

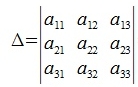(3a)

Элементы M_ij называются минорами элементов a_ij, и являются определителями матрицы (3), полученные вычеркиванием i-ой строки и j-го столбца.

Заметим, что выражение

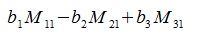
является определителем матрицы

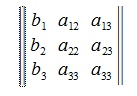
Если определитель (3a) неравен нулю, то x₁ вычисляется из следующего выражения:

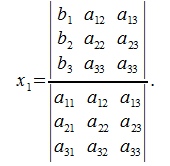
Аналогично вычисляются x₂ и x₃, умножая уравнения системы (2) на соответствующие выражения и суммируя:

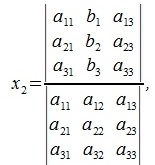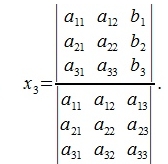Распространяя вышеизложенное на системы линейных уравнений с n неизвестными и n уравнениями можно сформулировать понятие определителя для квадратной матрицы порядка n.

Пусть задана матрица

(4)

Определителем порядка n, соответствующим матрице (4), называется число равное

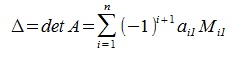(5)

Сделаем следующее обозначение:

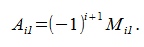
Тогда выражение (5) можно переписать в следующем виде:

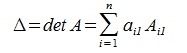(6)

A_ij называется алгебраическим дополнением элемента a_ij.

В вышеизложенном выражении определитель вычисляется суммируя произведения всех элементов первого столбца на соответствующие им алгебраические дополнения. Аналогично можно показать, что определитель равна сумме произведений всех элементов какой либо строки (или столбца) на соответствующие алгебраические дополнения:

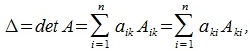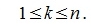(7)

Однако, для вычисления определителя матрицы большой размерности, такой подход требует больших усилий. Ниже мы представим более оптимальный метод вычисления определителя. Для этого сначала изложим некоторые важные свойства определителей.

Свойства определителей

1. Перестановка строк меняет знак определителя на обратное.
2. Общий для всех элементов множитель какой либо строки, можно выносить за знак определителя.
3. При сложении двух определителей, различающихся только одной строкой, соответствующие элементы этой строки складываются.
4. Прибавление одной строки к другой строке, умноженной на число, не изменяет значение определителя.
5. При замене местами строк и столбцов (при транспонировании) определитель не изменит своего значения.

Вычисление определителя матрицы с помощью исключения Гаусса

Для вычисления определителя приведем матрицу к верхнему треугольному виду с помощью исключения Гаусса. Тогда выражение (7) примет следующий вид:

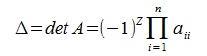(8)

где Z- общее количество перестановок. При каждой перестановке строк, изменяется знак определителя на обратное (свойство 1). Если общее число перестановок нечетное, то нужно поменять знак произведения элементов главной диагонали на обратное.

Онлайн нахождение определителя матрицы

Для нахождения определителя матрицы вы можете использовать матричный онлайн калькулятор. Для подробного решения используйте онлайн калькулятор для вычисления определителя матрицы.