Определение 1.1. Множество R элементов x, y, z, ... любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:
Элементы линейного (векторного) пространства называются векторами.
Определение 2.1. Совокупность линейно независимых элементов 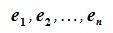 пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла
пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла 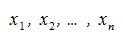 такие, что выполнено равенство
такие, что выполнено равенство
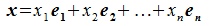 | (2.1) |
Равенство (2.1) называется разложением элемента x по базису 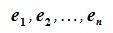 а числа
а числа 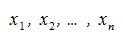 называются координатами элемента x (относительно базиса
называются координатами элемента x (относительно базиса 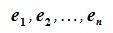 ).
).
Докажем, что любой элемент x линейного пространства R может быть разложен по базису 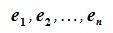 единственным образом.
единственным образом.
Пусть существует и другое разложение x:
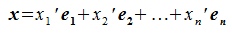 | (2.2) |
Вычитая (2.1) из (2.2) имеем:
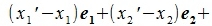 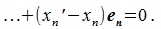 | (2.3) |
Так как базисные элементы 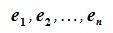 линейно независимы из соотношения (2.3) следует, что
линейно независимы из соотношения (2.3) следует, что
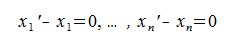
или
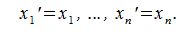
Следовательно каждый элемент линейного пространства R может быть разложен по базису 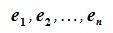 единственным образом.
единственным образом.
Теорема 2.2. При сложении произвольных двух элементов линейного пространства R их координаты (относительно любого базиса пространства R) складываются, а при умножении любого элемента x на любое число α все координаты x умножаются на α.
Доказательство следует из аксиом 1-8 определения 1.1.
Рассмотрим произвольное вещественное пространство R.
Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.
Размерность пространства обозначают символом dim.
Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.
Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис.
Доказательство. Так как R является n -мерным пространством, то из определения 2.1 следует, что в нем существует совокупность из n линейно независимых элементов 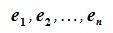 . Пусть x - любой элемент из R. Тогда согласно определению 3.1
. Пусть x - любой элемент из R. Тогда согласно определению 3.1 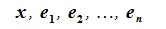 линейно зависимы, т.е. существуют числа
линейно зависимы, т.е. существуют числа 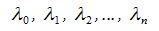 (не все равные нулю) такие, что справедливо равенство
(не все равные нулю) такие, что справедливо равенство
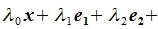 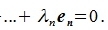 | (3.1) |
Заметим, что λ0≠0 т.к. в противном случае из равенства (3.1) следовала, что элементы 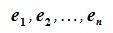 линейно зависимы. Поделив равенство (3.1) на λ0 и положив
линейно зависимы. Поделив равенство (3.1) на λ0 и положив
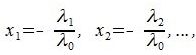 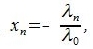 | (3.2) |
получим
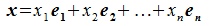 | (3.3) |
Из равенства (3.3) следует, что любой вектор из пространства R может быть разложен по элементам 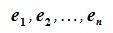 и, следовательно, они образуют базис пространства R. ■
и, следовательно, они образуют базис пространства R. ■
Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n).
Доказательство. Пусть множество n элементов 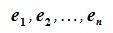 является базисом пространства R. Достаточно доказать, что любые n+1 элементы
является базисом пространства R. Достаточно доказать, что любые n+1 элементы 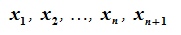 этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
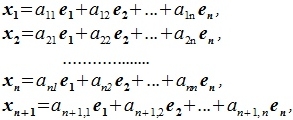 | (3.4) |
где a11, a12,..., an+1,n вещественные числа.
Пусть элементы 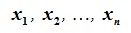 линейно независимы. Перепишем (3.4) в матричном виде:
линейно независимы. Перепишем (3.4) в матричном виде:
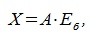 | (3.5) |
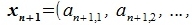 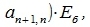 | (3.6) |
где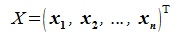 ,
,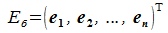 n×n-матрицы(элементы
n×n-матрицы(элементы 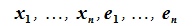 здесь являются вектор-строками),
здесь являются вектор-строками),
 | (3.7) |
Так как 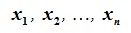 линейно независимы, матрица A имеет обратную матрицу A-1. Решив матричное уравнение (3.5) относительно
линейно независимы, матрица A имеет обратную матрицу A-1. Решив матричное уравнение (3.5) относительно 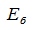 получим :
получим :
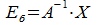 | (3.8) |
Подставляя (3.8) в (3.6), получим:
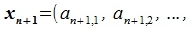 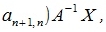 | (3.9) |
Как видно из уравнения (3.9) 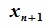 можно представить линейной комбинацией векторов
можно представить линейной комбинацией векторов 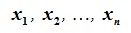 . Следовательно векторы
. Следовательно векторы 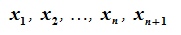 линейно зависимы. ■
линейно зависимы. ■
Пусть в пространстве R наряду с исходным базисом 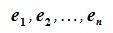 имеется другой базис
имеется другой базис 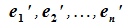 . Векторы этого базиса можно выразить через линейную комбинацию векторов исходного базиса следующим образом:
. Векторы этого базиса можно выразить через линейную комбинацию векторов исходного базиса следующим образом:
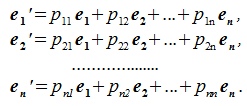 | (4.1) |
или
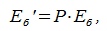 | (4.2) |
где 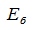 и
и 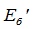 матрицы составленные из векторов строк
матрицы составленные из векторов строк 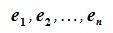 и
и 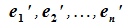 соответственно (
соответственно (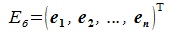
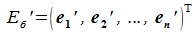 ), а матрица P имеет вид:
), а матрица P имеет вид:
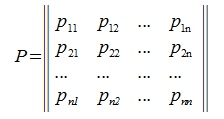 | (4.3) |
Матрица P называется матрицей замены базиса 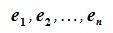 на
на 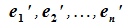 .
.
В свою очередь, векторы исходного базиса выражаются через векторы нового следующим соотношением:
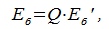 | (4.4) |
где
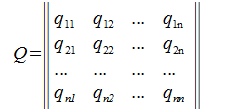 | (4.5) |
Подставляя (4.2) в (4.4) имеем:
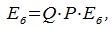 | (4.6) |
Из (4.6) следует, что QP=E, где E-единичная матрица, а матрицы Q и P взаимно обратные матрицы.
Рассмотрим как изменяются координаты векторов при замене базиса.
Пусть вектор x имеет координаты 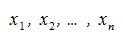 в базисе
в базисе 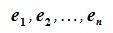 и координаты
и координаты 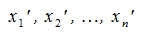 в базисе
в базисе 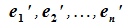 , тогда
, тогда
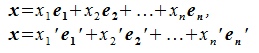 | (4.7) |
или
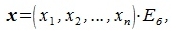 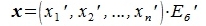 | (4.8) |
Из (4.8) и из (4.2) имеем:
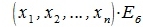 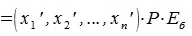 | (4.9) |
Так как 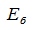 квадратная матрица полного ранга, она имеет обратную матрицу. Умножив левые и правые части уравнения (4.9) на обратную к
квадратная матрица полного ранга, она имеет обратную матрицу. Умножив левые и правые части уравнения (4.9) на обратную к 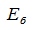 матрицу получим:
матрицу получим:
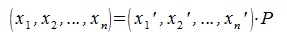
или
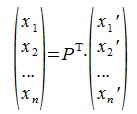 | (4.10) |
Матрица PT называется матрицей преобразования координат. Она транспонирована с матрицей замены базиса. Обратная матрица (PT)-1 дает выражения новых координат через старые.
Матрица, обратная к транспонированной для некоторой матрицы, называется контраградиентной с ней.
Определение 5.1. Два произвольных вещественных линейных пространства R и R' называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если x, y∈R отвечают x', y'∊R' соответственно, то элементу x+y∈R отвечает элемент x'+y'∈R', а для любого вещественного α, элементу αx∈R отвечает элемент αx'∈R'.
Теорема 5.2. Если пространства R и R' изоморфны, то они имеют одинаковую размерность.
Доказательство. Пусть линейные пространства R и R' изоморфны, и пусть элементам 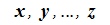 пространства R отвечают элементы
пространства R отвечают элементы 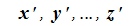 пространства R' соответственно. Допустим элементы
пространства R' соответственно. Допустим элементы 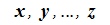 линейно независимы. Покажем, что элементы
линейно независимы. Покажем, что элементы 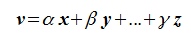 также линейно независимы. Исходя из обратного предположения допустим, что элементы
также линейно независимы. Исходя из обратного предположения допустим, что элементы 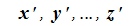 линейно зависимы. тогда один из них можно представить линейной комбинацией остальных элементов:
линейно зависимы. тогда один из них можно представить линейной комбинацией остальных элементов: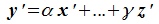 . Но элементам
. Но элементам 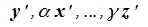 отвечают элементы
отвечают элементы 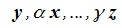 y в пространстве R, а сумме
y в пространстве R, а сумме 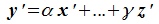 отвечает сумма
отвечает сумма 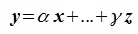 . Но последнее означает линейную зависимость элементов
. Но последнее означает линейную зависимость элементов 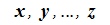 . Следовательно
. Следовательно 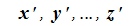 линейно независимы. Из линейной зависимости элементов
линейно независимы. Из линейной зависимости элементов 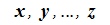 следует линейная зависимость элементов
следует линейная зависимость элементов 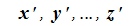 . Следовательно максимальное количество линейно независимых векторов для пространств R и R' одно и то же, т.е. эти пространства имеют одинаковую размерность. ■
. Следовательно максимальное количество линейно независимых векторов для пространств R и R' одно и то же, т.е. эти пространства имеют одинаковую размерность. ■
Теорема 5.3. Любые два n-мерных вещественных линейных пространства R и R' изоморфны.
Доказательство. Выберем базисы 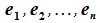 и
и 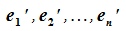 для пространств R и R' соответственно. Тогда каждый элемент пространства R можно представить линейной комбинацией базисных элементов:
для пространств R и R' соответственно. Тогда каждый элемент пространства R можно представить линейной комбинацией базисных элементов: 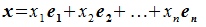 . Этому элементу в пространстве R' поставим в соответствие элемент теми же координатами:
. Этому элементу в пространстве R' поставим в соответствие элемент теми же координатами: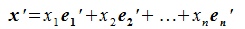 . В свою очередь элементу x' пространства R' соответствует элемент x пространства R . Отметим, что если элементам x и y пространства R отвечают элементы x' и y' пространства R' соответственно , то исходя из теоремы 2.2 элементу x+y пространства R отвечает элемент x'+y' пространства R', а элементу αx отвечает элемент αx'. ■
. В свою очередь элементу x' пространства R' соответствует элемент x пространства R . Отметим, что если элементам x и y пространства R отвечают элементы x' и y' пространства R' соответственно , то исходя из теоремы 2.2 элементу x+y пространства R отвечает элемент x'+y' пространства R', а элементу αx отвечает элемент αx'. ■