Обратная матрица. Нахождение обратной матрицы

Пусть A невырожденная n×n матрица. Тогда для нее существует матрица A^-1 такая, что

AA^-1=A^-1A=E,

где E - единичная матрица.

A^-1 называется обратной к матрице A.

Нахождение обратной матрицы

Пусть задана матрица A порядка n×n и пусть ранг матрицы A :

rank A=n.

Из определения обратной матрицы имеем:

A^-1A=E

или

AA-1=E ,

(1)

где E − единичная матрица, A^-1 − обратная к матрице A.

Для нахождения обратной матрицы A^-1, перепишем матричное уравнение (1) в виде

Ax1=e1, Ax2=e2, ......... Axn=en,

(2)

где xⁱ − i-ый вектор столбец матрицы A^-1, которую нужно найти, eⁱ − i-ый вектор столбец единичной матрицы.

Таким образом для нахождения обратной матрицы A^-1 нужно вычислить векторы столбцы xⁱ для n систем линейных уравнений (2).

Рассмотрим первую систему линейных уравнений:

Ax1=e1.

(3)

Для решения системы линейных уравнений (3) относительно x¹ воспользуемся методом Гаусса.

Аналогичным образом решаются остальные системы линейных уравнений (2).

Наконец группа векторов столбцов x¹, x², ..., xⁿ образует обратную матрицу A^-1.

Заметим, что один раз находя матрицы перестановок P₁,P₂, ... , P_n-1 и матрицы исключений М₁, М₂, ..., M_n-1 (см. страницу Метод исключения Гаусса) и построив матрицу

M=M_n-1P_n-1...M₂P₂M₁P₁,

систему (2) можно преобразовать к виду

Отсюда находятся x¹,x², ..., xⁿ, при разных правых частях Me¹, Me², ..., Meⁿ.

При вычислении обратной матрицы более удобно с правой стороны исходной матрицы добавить единичную матрицу и применять метод Гаусса в прямом и обратном направлениях.

Рассмотрим это на примере.

Пример вычисления обратной матрицы

Пусть требуется найти обратную матрицу A^-1 для данной матрицы A:

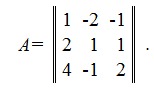
Запишем с правой стороны единичную матрицу:

Выбираем ведущий элемент "4" (т.к. он самый большой по модулю) и переставляем местами первую и третью строки:

Применяем Гауссово исключение для первого столбца:

Переставляем вторую и третью строки и применяем Гауссово исключение для второго столбца:

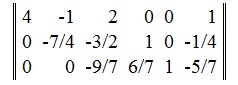
Третью строку делим на -9/7:

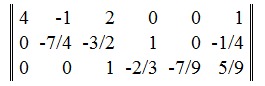
Далее применяем Гауссово исключение в обратном порядке, т.е. третью строку оставляем без изменения, вторую строку суммируем с третьим умноженным на 3/2, первую суммируем с третьим умноженным на -2:

Вторую строку делим на -7/4:

Суммируем первую и вторую строки:

Делим первую строку на "4":

Таким образом, правая часть полученной матрицы и есть искомая обратная к матрице A:

Онлайн нахождение обратной матрицы

Для нахождения обратной матрицы используйте матричный онлайн калькулятор . Для подробного решения используйте калькулятор для вычиления обратной матрицы.