Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку "Вычислить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Рассмотрим следующую систему линейных уравнений:
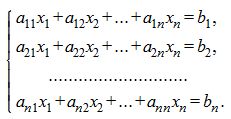 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
где
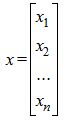 | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
| A−1Ax=A−1b. | (4) |
Учитывая определение обратной матрицы, имеем A−1A=E, где E- единичная матрица. Следовательно (4) можно записать так:
| Ex=A−1b. | (4) |
или, учитывая, что Ex=x:
| x=A−1b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Пример 1. Решить следующую систему линейных уравнений матричным методом:
Матричный вид записи системы линейных уравнений: Ax=b, где
| . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
| . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
| . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
| . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
| . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
| . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
| . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
| . |
Ответ:
Пример 2. Решить следующую систему линейных уравнений матричным методом:
| . |
Матричный вид записи системы линейных уравнений: Ax=b, где
| . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
| . |
Вычислим все алгебраические дополнения матрицы A:
| , |
| , |
| , |
| , |
| , |
| , |
| , |
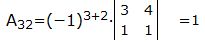 , , |
| . |
Обратная матрица вычисляется из следующего выражения:
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
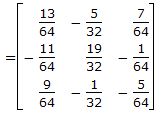 |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
Ответ: